|
Volumen 12, Número 2, Abril-Junio, 2024, Páginas 115 al 127 |
|
ARTÍCULO ORIGINAL
Aplicación de los modelos
experimentales de Peleg y Page durante la
deshidratación osmótica y el secado convectivo de mitades de tomate (Solanum lycopersicum L.)
Application of Peleg and Page's
experimental models during osmotic dehydration and convective drying of tomato
halves (Solanum lycopersicum L.)
Luis
Soto-Jiménez[1]![]() *, Cesar
Monteza-Arbulú 1
*, Cesar
Monteza-Arbulú 1![]() y Miguel Angel Solano-Cornejo1
y Miguel Angel Solano-Cornejo1 ![]() .
.
RESUMEN
El fenómeno de la transferencia de masa durante la
deshidratación osmótica y secado convectivo de mitades de tomates (Solanum lycopersicum
L.) se llevó a cabo 1) utilizando sacarosa y sal como solutos; 2) ajustando las
ecuaciones de Peleg y Page a los datos
experimentales. La fruta se cortó en mitades y se extrajo sus semillas y
placenta. Se la deshidrató osmóticamente con soluciones: al 10.8% 18% y al 30%
50%, (p/v), de sal y sacarosa respectivamente a temperatura de 25 °C.
Posteriormente, las muestras resultantes, fueron sometidas a un proceso de
secado convectivo por aire forzado en un túnel a las temperaturas de: 50; 70;
90 °C. Determinándose la pérdida de peso de las muestras, la ganancia de
sólidos, obteniendo parámetros de los modelos experimentales de Peleg y Page con niveles de correlación de R2 ≥0.9894 para
los modelos propuestos.
Palabras clave: tomate, transferencia de masa,
deshidratación osmótica, secado, modelos matemáticos
ABSTRACT
The phenomenon of mass transfer during
osmotic dehydration and convective drying of tomato halves (Solanum lycopersicum L.) was carried out 1) using sucrose and
salt as solutes; and 2) by fitting the Peleg and Page equations to the
experimental data. The fruit was cut into halves and its seeds and placenta
were removed. It was osmotically dehydrated with solutions: 10.8% 18% and 30%
50%, (w/v), of salt and sucrose respectively at a temperature of 25 °C.
Subsequently, the resulting samples were subjected to a convective drying
process by forced air in a tunnel at temperatures of: 50; 70 and 90ºC.
Determining the weight loss of the samples, the solids gain, obtaining
parameters from the experimental models of Peleg and Page with correlation
levels of R2 ≥0.9894 for the proposed models.
Keywords: tomato, mass
transfer, osmotic dehydration, drying, mathematical models
* Autor para correspondencia
INTRODUCCIÓN
En la actualidad es importante para
el consumidor ingerir alimentos, que además de sus beneficios nutricionales
originales, éstos ayuden a mantener la salud en la prevención de enfermedades;
buena parte de la producción mundial de frutas y hortalizas entre ellos el
tomate está siendo vista con atención como un alimento funcional (Milacatl, 2003). El problema del tomate es que es altamente
perecible. Dicho problema se debe a una combinación de factores biológicos,
físicos y químicos que contribuyen al deterioro después de la cosecha
(Hernández et al., 2011). Los tomates son productos hortofrutícolas sensibles
al deterioro por su alto contenido de agua, baja resistencia estructural y su
naturaleza respiratoria activa (Neumann, 2021; De Icaza, 2018).
Los tomates después de su cosecha
continúan respirando, proceso que implica el consumo de oxígeno y producción de
dióxido de carbono y agua. Este proceso es relevante para mantener las
funciones vitales del fruto, sin embargo, también implica una pérdida de
reservas alimenticias que reduce la vida útil (De Icaza, 2018 ). El tomate
también continúa madurando después de su cosecha (fruto climatérico), sobre
todo si no se controla el Etileno que libera del fruto, acerándose la
maduración y deterioro (Firdous et al., 2022). Los
tomates son susceptibles a daños físicos por su textura blanda; cuando estos
daños ocurren incrementa la posibilidad del deterioro por acciones de
microorganismos (Neumann, 2021).
Una de las alternativas de solución
a la perecibilidad del tomate es la reducción de la humedad. Por ejemplo, la
deshidratación osmótica (DO) es un proceso ampliamente estudiado en los últimos
años y usado principalmente como pre-tratamiento de
muestras que luego son sometidas a congelación o a deshidratación térmica (como
el secado por convección
La aplicación deshidratación
osmótica es simple y de bajo costo, debido entre otros al menor requerimiento
de energía, brinda la posibilidad de preservar alimentos altamente perecederos,
como el tomate
Durante la deshidratación osmótica
ocurren varios fenómenos de transferencia de masa como el flujo de agua del
producto hacia el medio osmótico; la diferencia en la concentración de solutos
entre el alimento y la solución osmótica crea un gradiente osmótico que impulsa
la salida de agua desde el alimento hacia la solución (Aquino, 2023). Asimismo,
ocurre el fenómeno de ingreso de solutos desde la solución osmótica al
producto; simultáneamente a la pérdida de agua del alimento, los solutos de la
solución osmótica (como azúcar o sal), pueden transferirse hacia el interior
del alimento a una velocidad que dependen de la diferencia de concentración, la
temperatura de la solución, las propiedades físicas del alimento, y el tiempo
de procesamiento (Pinzon, 2011).
Por lo general después del proceso
de deshidratación osmótica, sigue una deshidratación térmica complementaría,
como el secado por convección que es ampliamente utilizado. Este proceso
implica la transferencia de masa y energía entre el producto y el aire
circulante con el objetivo de eliminar suficiente contenido de agua hasta reducir
la actividad del agua a un nivel que impida el crecimiento de microorganismos y
la degradación enzimática (García et al., 2015).
La temperatura de secado después de
la deshidratación osmótica es importantísima, la pérdida de humedad se
incrementará proporcionalmente al aumento de la temperatura de secado; por lo
que para elegir la temperatura adecuada del proceso se debe considerar la
composición del alimento
Se han aplicado diferentes modelos
matemáticos para ajustar los resultados experimentales de procesos de la
deshidratación osmótica, con el objeto de predecir el comportamiento de los
productos alimenticios en la pérdida de humedad y ganancia de sólidos, por lo
que se considera de suma importancia conocer los parámetros para su
procesamiento. Unos de los modelos más usados son las ecuaciones propuestas por
Peleg y Page para predecir los parámetros señalados
anteriormente (Petrotos y Lazarides,
2001; Della-Rocca y Mascheroni, 2011). La deshidratación
osmótica (DO) se ha considerado como un pretratamiento que cambia la condición
del alimento sometido a secado sucesivo en términos no solamente en proporción
de agua a materia seca, pero también propiedades físicas y composición química
A pesar de sus ventajas, la
deshidratación osmótica (DO) aún tiene restricciones para su implementación a
nivel industrial tanto en el diseño de los equipos como de los procesos. Estas
restricciones están relacionadas principalmente con la falta de modelos predictivos
de cinéticas de pérdida de humedad y ganancia de sólidos que permitan
relacionar con precisión las características de los productos deshidratados con
las de la materia prima y las variables del proceso. Aunque la deshidratación
osmótica ha sido utilizada desde muchos años atrás, generalmente se ha
trabajado en forma empírica y la información experimental se interpreta con
modelos que son válidos solamente para reproducir condiciones semejantes a las
del trabajo del cual fueron obtenidos (Barat, 1998).
Por ello, el objetivo de este estudio fue determinar el modelamiento matemático
de la transferencia de masa durante la deshidratación osmótica y el secado
convectivo del tomate variedad río grande, utilizando como solutos sal y
sacarosa para luego evaluar el ajuste de los resultados experimentales a
modelos matemáticos preestablecidos; como el modelo de Peleg
y Page; para la deshidratación osmótica y secado convectivo respectivamente.
MATERIALES Y
MÉTODOS
Preparación de la muestra
Se seleccionaron y compraron tomates
de la variedad “Río Grande” en el Mercado Modelo de Lambayeque. Se lavaron y
desinfectaron, el agua a usar fue agua destilada distribuida en el laboratorio
de Química Orgánica FIQIA-UNPRG, para su desinfección se usó desinfectante
orgánico en la dosis (10 mL del producto / L de agua).
Se procedió a cortar los tomates en
mitades, de manera longitudinal, se retiraron las pepas y la placenta con
cuidado de no dañar las paredes del tomate, se pesó y rotuló las mitades de
tomates; las muestras fueron caracterizadas acidez titulable por titulación con
NaOH al 0.1 N (AT), humedad por secado en estufa (H) y sólidos totales por
refractometría (SST).
Procedimiento de deshidratación osmótica
Se prepararon soluciones de sal
(NaCl) y sacarosa al 10.8, 18%, 30 y 50 % (p/v). Las mitades de tomates fueron
colocadas en las soluciones de sal o sacarosa controlándose el peso cada hora
extrayendo muestras al azar; para determinar peso y humedad hasta completar las
5 horas de deshidratación osmótica.
Procedimiento de Secado
Posterior a la deshidratación
osmótica las muestras fueron secadas en aire a 50, 70 y 90 °C; para ello el
tomate fue colocado en bandejas, dentro del secador por aire forzado perteneciente
al laboratorio de procesos unitarios de la universidad nacional Pedro Ruiz
Gallo. Durante las 10 horas de secado al aire se extrajeron 04 muestras de
tomates al azar por cada hora de secado hasta concluir el proceso.
Cálculo de parámetros de transferencia
de masa
Para el cálculo de los parámetros de
transferencia de masa se utilizaron las siguientes ecuaciones de acuerdo a lo
indicado por
![]()
![]()
![]()
![]()
Donde:
Wi
= peso de la muestra inicial en g;
Wt
= peso de la muestra al tiempo t en g;
SSi
= sólidos solubles iniciales (°Brix) expresados en g sólidos/100 g–1 MF;
SSt
= sólidos solubles al tiempo t (°Brix t) expresados en g sólidos/100 g–1 MF;
Mi
= humedad inicial expresada en g H2O/100 g–1 MF;
Mt
= humedad al tiempo t expresada en g H2O/100 g–1 MF
Modelado matemático por ecuación de Peleg de deshidratación osmótica
La ecuación de Peleg
(1988), describe las curvas que se acercan a un equilibrio asintótico. Es un
modelo no-exponencial de dos parámetros según lo indicado por
![]()
Donde:
Mi
= humedad inicial;
M
(t) = humedad al tiempo t;
k1
= Constante de Velocidad de Peleg
(min g/g-1)
k2
= Constante de Capacidad de Peleg
(g/g)-1
Similar
ecuación se puede escribir para la ganancia de sólidos (SG) y para la pérdida
de peso
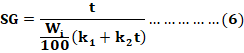
En las ecuaciones 5 y 6 las
constantes de Peleg (k1 y k2) y
el coeficiente de correlación para dada temperatura y soluto (sal o sacarosa),
se determinaron por regresión lineal, utilizándose posteriormente en el
modelamiento con las ecuaciones (5) y (7). Obtenidos los valores de las
constantes del modelo de Peleg, se modelaron las
curvas de deshidratación osmótica comparándolas con los valores experimentales
obtenidos.
Modelado matemático por ecuación de Page
de deshidratación convectiva por aire
Para el comportamiento del proceso
de secado se ha modelado utilizando la ecuación de Page, de acuerdo a lo
indicado por
![]()
Donde:
![]() Relación de humedad,
Relación de humedad,
![]() : Contenido de humedad en un
instante cualquiera (%),
: Contenido de humedad en un
instante cualquiera (%),
![]() : Contenido de humedad inicial (%),
: Contenido de humedad inicial (%),
![]() Contenido de humedad en equilibrio (%),
Contenido de humedad en equilibrio (%),
![]() : Tiempo (min),
: Tiempo (min),
![]() : Coeficiente del modelo de Page,
: Coeficiente del modelo de Page,
![]() : Constante del modelo de Page
: Constante del modelo de Page
En la ecuación (7) el Coeficiente y
la Constante de la ecuación de Page (k y n) fueron estimados por Regresión
lineal, una vez obtenidos los valores del Coeficiente y Constantes del modelo de
Page, permitieron construir las curvas de secado convectivo, y se compararon
con los valores experimentales.
Análisis Estadístico
Se determinaron las diferencias
significativas utilizando el Análisis de Varianza (ANVA) para un diseño
completamente al azar (DCA), y para los valores que presentaron diferencia
significativa (p>0.05) se realizaron comparaciones pareadas
por el método de Tukey (p> 0.05), tal como indica
RESULTADOS
Deshidratación
osmótica (DO) de tomate
Los resultados de la deshidratación osmótica de
tomate utilizando soluciones de sal (10.8 y 18%) y sacarosa (30 y 50%) se
presentan en la Figura 1. Así mismo se presenta la variación de humedad
predicha por la ecuación de Peleg.
Figura 1
Modelamiento
de la Variación de la Humedad en Base Humedad (HBH) en tomate por
deshidratación osmótica basado en la Ecuación de Peleg
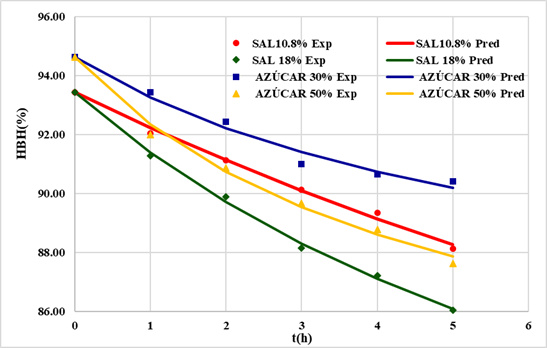
Se puede observar que conforme progresa el contacto
entre la solución osmótica y el tomate la humedad disminuye; así mismo conforme
la concentración del soluto osmótico (sal o sacarosa) aumenta la velocidad de
deshidratación aumenta y la humedad final disminuye.
Los parámetros de modelamiento de la perdida de
humedad usando la ecuación de Peleg se presentan en
la Tabla 1. En ella podemos observar que la ecuación de Peleg
presenta un alto nivel de ajuste a los datos experimentales (R2 ≥ 0.989)
|
Constantes de Peleg
y Coeficiente de Correlación en el Modelamiento de la Variación de Humedad por
la Ecuación de Peleg |
||||
|
Valores |
Sal 10.8% |
Sal 18% |
Azúcar 30% |
Azúcar 50% |
|
k1 |
0.801608 |
0.443618 |
0.635555 |
0.363547 |
|
k2 |
0.032935 |
0.047179 |
0.098480 |
0.075170 |
|
R2 |
0.997466 |
0.998934 |
0.989457 |
0.996147 |
Los valores de humedad final por
deshidratación osmótica en sal y azúcar se presentan en la Tabla 02
|
Tabla 2 Humedad final en tomate osmodeshidratado
por 5 horas con diferentes soluciones osmóticas. (p>0.05) |
|||
|
Soluciones |
Conteo |
Medias |
Grupos
homogéneos |
|
Sal 18% |
6 |
85.5333 |
X |
|
Azúcar 50% |
6 |
87.0583 |
X |
|
Sal 10.8% |
6 |
88.0883 |
X |
|
Azúcar 30% |
6 |
89.8100 |
X |
Los efectos de la deshidratación osmótica de tomate
sobre la ganancia de solidos utilizando soluciones de sal (10.8 y 18%) y
sacarosa (30 y 50%) se presentan en la figura 02. Así mismo se presenta los
valores predichos de ganancia de solidos de acuerdo a la ecuación de Peleg.
Figura 2
Modelamiento de la
Ganancia de Solidos (%) en tomate por deshidratación osmótica basado en la
Ecuación de Peleg
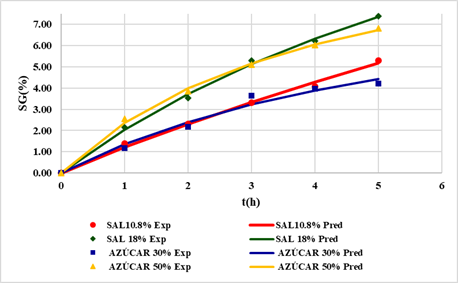
Se puede observar que conforme el tiempo de contacto
tomate: solución osmótica la ganancia de sólidos aumenta; así mismo se
determinó que conforme aumenta la concentración del soluto osmótico (sal o
sacarosa) aumenta la velocidad de ganancia de peso y la ganancia final de
sólidos también aumenta.
Los parámetros de modelamiento de la ganancia de
solidos usando la ecuación de Peleg se presentan en
la Tabla 3. En ella podemos observar que la ecuación de Peleg
presenta un alto nivel de ajuste a los datos experimentales (R2 ≥ 0.989)
|
Tabla 3 Constantes de Peleg y coeficiente
de correlación en el modelamiento de la ganancia de sólidos por la ecuación
de Peleg |
||||
|
Valores |
Sal 10.8% |
Sal 18% |
Azúcar 30% |
Azúcar 50% |
|
k1 |
0.801608 |
0.443618 |
0.635518 |
0.342836 |
|
k2 |
0.032935 |
0.047179 |
0.098484 |
0.079706 |
|
R2 |
0.997466 |
0.998934 |
0.989458 |
0.999042 |
Los
valores de %ganancia de sólidos (%SG) por deshidratación osmótica en sal y
azúcar se presentan en la Tabla 04
|
Tabla 4 Ganancia de sólidos en tomate osmodeshidratado por 5 horas con diferentes soluciones
osmóticas. (p>0.05) |
|||
|
Soluciones |
Conteo |
Medias |
Grupos homogéneos |
|
Azúcar
30% |
6 |
4.43833 |
X |
|
Sal
10.8% |
6 |
5.21833 |
X |
|
Azúcar
50% |
6 |
6.74000 |
X |
|
Sal
18% |
6 |
7.33333 |
X |
Se determinó que con 5 horas de deshidratación osmótica la solución de
sal al 18% logró la mayor ganancia de sólidos; seguida por la solución de
azúcar al 50% y sal al 10.8% ambas sin presentar diferencias significativas
entre sí; siendo la de menor ganancia de sólidos la solución de azúcar al 30%.
Deshidratación convectiva de tomate osmodeshidratado
La variación de la relación de humedad (MR) durante el proceso de secado
convectivo a 50, 70 y 90 °C de tomate osmodeshidratado
con diferentes soluciones se presenta en la figura 03. Se presentan así mismo
los valores de MR predichos por la ecuación de Page.
Figura 3
Modelamiento
del secado convectivo de tomate osmodeshidratados
basado en la ecuación de Page
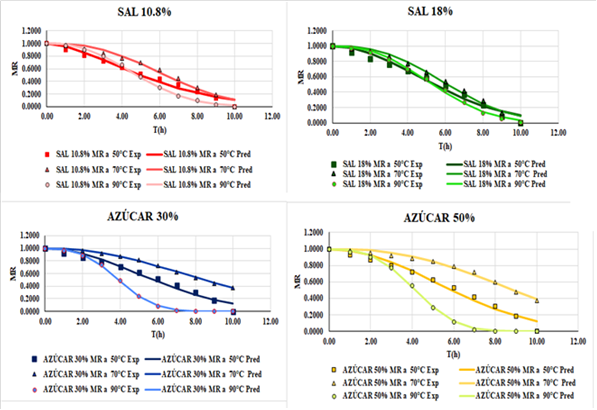
Se puede observar que conforme aumenta la
temperatura y el tiempo de secado; la pérdida de humedad es mayor. Todas las
curvas de secado presentan una forma sigmoidea similar, aunque diferentes en el
grado de la pendiente y en el tiempo de llegar a la humedad de equilibrio. En
términos generales los tomates osmodeshidratados
previamente en soluciones osmóticas con sacarosa presentaron bajadas de humedad
más pronunciadas en tomates osmodeshidratados a
mayores temperaturas. En este caso, los tomates a temperaturas de 90°C
presentan un descenso más pronunciado entre 7 h para los tomates osmodeshidratados en azúcar 30 y 50% y en el caso de sal
10.8 y 18% necesitaron de 9 horas.
Los
parámetros de modelamiento de secado convectivo usando la ecuación de Page se
presentan en la Tabla 5. En ella podemos
observar que la ecuación de Page presenta un alto nivel de ajuste a los datos
experimentales, determinaron las constantes de secado (k y n), coeficiente de
correlación(R2), obteniéndose R2≥0.985.
|
Tabla 5 Constantes de secado,
coeficiente de correlación. Modelo Page. |
||||||||||||
|
Ctes de Secado |
k |
n |
R2 |
k |
N |
R2 |
k |
N |
R2 |
k |
n |
R2 |
|
T(°C) |
sal 10.8% |
sal 18% |
azúcar 30% |
azúcar 50% |
||||||||
|
50 |
0.050 |
1.642 |
0.988 |
0.024 |
1.981 |
0.986 |
0.022 |
1.977 |
0.985 |
0.017 |
2.079 |
0.985 |
|
70 |
0.007 |
2.534 |
0.990 |
0.007 |
2.558 |
0.994 |
0.007 |
2.146 |
0.999 |
0.003 |
2.508 |
0.994 |
|
90 |
0.015 |
2.454 |
0.999 |
0.011 |
2.498 |
0.998 |
0.013 |
2.893 |
0.999 |
0.009 |
3.024 |
0.999 |
DISCUSIÓN
Se obtuvieron parámetros fisicoquímicos iniciales en
los tomates antes de la DO: %H inicial: 94.506±0.68, acidez
titulable (A.T. prom= 0.029 ±0.01),
sólidos solubles totales (S.S.T.= 3.505±0.003), pasada la DO y el secado
convectivo se obtuvo mitades de tomates osmodeshidratados
con 7.01 %H y 5.310 % de ganancia de sólidos (%SG).
Durante las cinco horas de DO, el contenido de
soluto de las zonas internas aumentó con el tiempo del proceso, debido a
difusión desde las capas externas, similar a lo reportado por Goula & Lazarides, (2012), que deshidrataron de 3 a 4 horas, por lo
tanto, la penetración de solutos en el producto durante los períodos osmóticos
utilizados solo es importante para la zona subsuperficial, estos autores
sostienen además que el modelo logarítmico permite una descripción general de
la cinética de secado, sin embargo, para nuestra investigación usando la
ecuación de Peleg, también puede describir como se
comportará el fenómeno de transferencia de masa en la deshidratación osmótica.
Se obtuvo pérdidas de agua (%WL) de 4.70%, 6.42%,
7.45% y 8.98% en las soluciones de azúcar 30%, sal 10.8%, azúcar 50% y
finalmente sal 18%, respectivamente, la solución de NaCl al 18% p/v fue la que logró mayor pérdida de agua en
las mitades del tomate variedad Río Grande , coincidiendo en lo
reportado por Li et al., (2012), que sostiene que los valores de la WL en
tomates Cherry tratados con ultrasonido a 150 W durante 30 min, aumentaron a
medida que aumentó la concentración de cloruro de sodio, lo que puede
atribuirse al aumento de la presión osmótica con el aumento de la concentración
de sal.
Para el proceso de secado convectivo,
las temperaturas usadas fueron 50, 70 y 90 ºC, éstas establecieron diferentes
comportamientos en sus curvas de secado, coincidiendo con lo reportado por Lewicki et al., (2002), en su estudio emplearon
cuartos de tomate , con diferentes soluciones osmóticas como pretratamiento al
secado convectivo, se usaron dos variedades de tomates: Lima y revermun, la temperatura de secado fue 60 ºC con variaciones de tiempo de 7 a 10 h, la variedad de tomate Lima se secó con
placenta y semillas, secándose mucho más
rápido que la v. Revermun, la diferencia parece deberse a diferentes
preparaciones de soluciones osmóticas como pretratamiento de los tomates para
secar, para nuestro caso se secaron mitades de tomates v. Río grande. Las
diferencias en la estructura y el contenido de agua de la placenta y el
pericarpio se reflejaron en la cinética y la repetibilidad del proceso de
secado.
CONCLUSIONES
El modelo
experimental de Peleg para el fenómeno de
transferencia de masa de las mitades de tomates en las soluciones osmóticas de
sal y sacarosa arrojan un coeficiente de relación alto, de igual forma, para
modelar el secado convectivo aplicando Page en tomates osmodeshidratados
tuvo R2≥0.985.
REFERENCIAS
BIBLIOGRÁFICAS
Andritsos, N., Dalampakis, P., &
Kolios, N. (2003). Use of geothermal energy for tomato drying. Oregon Institute of Technology Geo-Heat
Center Bulletin.. https://bit.ly/4cuROk9
Aquino de los Santos C., Luján
Hidalgo, M., Ventura Canseco., & Abud Archila, M.. (2023). Deshidratación
osmótica de Carica papaya var. Maradol: Transferencia de masa y análisis
sensorial. ESPACIO I+D: Innovación Más Desarrollo, 11(31). https://doi.org/10.31644/IMASD.31.2022.a08
Barat, J.M. 1998. Desarrollo de un
modelo de la deshidratación osmótica como operación básica. [Tesis Doctoral,
Universidad Politécnica de Valencia]. https://riunet.upv.es/bitstream/handle/10251/1834/tesisUPV2195.pdf?sequence=1
De Icaza Tena, G.. (2018). La Vida
Útil de los Alimentos y sus Principales Reacciones. Innovación Editorial
Lagares de México, S.A. de C.V. https://books.google.com.pe/books?id=llN1DwAAQBAJ&printsec=frontcover&hl=es&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false
Della-Rocca, P., & Mascheroni, R.
(2011). Deshidratación de papas por métodos combinados de secado:
deshidratación osmótica, secado por microondas y convección con aire caliente.
Universidad Tecnologica Nacional, 9(2), 1–16. http://hdl.handle.net/11336/111733
Firdous, N., Khan, M. R., Butt, M.
S., Ali, M., Asim Shabbir, M., Din, A., Hussain, A., Siddeeg, A., &
Manzoor, M. F. (2022). Effect of Aloe vera gel-based edible coating on
microbiological safety and quality of tomato. CyTA: Journal of Food, 20(1),
355–365. https://doi.org/10.1080/19476337.2022.2136760
Ganjloo, A., Rahman, R. A., Bakar,
J., Osman, A., & Bimakr, M. (2012). Kinetics Modeling of Mass Transfer
Using Peleg’s Equation During Osmotic Dehydration of Seedless Guava (Psidium
guajava L.): Effect of Process Parameters. Food and Bioprocess
Technology, 5(6), 2151–2159. https://doi.org/10.1007/s11947-011-0546-2
Ganjloo, A., Rahman, R. A., Bakar,
J., Osman, A., & Bimakr, M. (2012). Kinetics Modeling of Mass Transfer
Using Peleg’s Equation During Osmotic Dehydration of Seedless Guava (Psidium
guajava L.): Effect of Process Parameters. Food and Bioprocess
Technology, 5(6), 2151–2159. https://doi.org/10.1007/s11947-011-0546-2
García-Paternina, M., Alvis-Bermudez,
A., & García-Mogollon, C. A. (2015). Evaluación de los Pretratamientos de
Deshidratación Osmótica y Microondas en la Obtención de Hojuelas de Mango
(Tommy Atkins). Información Tecnológica, 26(5), 63–70. https://doi.org/10.4067/S0718-07642015000500009
Gaware, T. J., Sutar, N., &
Thorat, B. N. (2010). Drying of tomato using different methods: Comparison of
dehydration and rehydration kinetics. Drying Technology, 28(5),
651–658. https://doi.org/10.1080/07373931003788759
Goula, A. M., & Lazarides, H. N.
(2012). Modeling of mass and heat transfer during combined processes of
osmotic dehydration and freezing (Osmo-Dehydro-Freezing). Chemical Engineering
Science, 82, 52–61. https://doi.org/10.1016/j.ces.2012.07.023
Hawkes J., Flink J., (1978); Osmotic
concentration of fruits slices prior to freeze dehydration. J. Food
Proc. Preserv. 2, pags. 265-284 https://doi.org/10.1111/j.1745-4549.1978.tb00562.x
Hernández, P. L. B., Delgado, A. C.
B., Sánchez, S. A. M., Castillo, H. S. V., & Porras, D. P. N. (2011). Efecto
del recubrimiento a base de almidón de yuca modificado sobre la maduración del
tomate. Revista Lasallista de Investigación, 8(2), 96–103. https://www.redalyc.org/pdf/695/69522607011.pdf
Lazarides, H.N.; Katsanidis, E. &
Nickolaidis, A. (1995). Mass transfer kinetics during osmotic preconcentration aiming
at minimal solid uptake. Revista de Ingeniería de Alimentos. 25(2), pags. 151-166. https://doi.org/10.1016/0260-8774(94)00006-U
Lewicki, P. P., Le, H. V., &
Pomara N Nska-Łazuka, W. (2002). Effect of pre-treatment on convective drying of
tomatoes. 1–6. www.elsevier.com/locate/jfoodeng
Li, H., Zhao, C., Guo, Y., An, K.,
Ding, S., & Wang, Z. (2012). Mass transfer evaluation of ultrasonic
osmotic dehydration of cherry tomatoes in sucrose and salt solutions.
International Journal of Food Science and Technology, 47(5), 954–960. https://doi.org/10.1111/j.1365-2621.2011.02927.x
Mariem, S., & Mabrouk, S. (2014).
Drying Characteristics of Tomato Slices and Mathematical Modeling.
International Journal of Energy Engineering, 2014(2A), 17–24. https://doi.org/10.5923/j.ijee.201401.03
Milacatl, V.; (2003); Cambios en
atributos sensoriales y degradación de ácido ascórbico en función de la
temperatura en puré y néctar de mango. [Tesis de grado. Universidad de las
Américas. Puebla, México]. http://catarina.udlap.mx/u_dl_a/tales/documentos/lia/milacatl_h_v/
Hayes, W.A., Smith, P.G., Morris
A.E., (2010). The production and
quality of tomato concentrates. Crit.Rev. Food Sci. Nutr., 7, pags. 537-564. https://doi.org/10.1080/10408699891274309
Nowicka, P., Wojdyło, A., Lech, K.,
& Figiel, A. (2015). Influence of Osmodehydration Pretreatment and
Combined Drying Method on the Bioactive Potential of Sour Cherry Fruits. Food
and Bioprocess Technology, 8(4), 824–836. https://doi.org/10.1007/s11947-014-1447-y
Neumann, L. (2021). Tópicos En Microbiología E Inocuidad
De Los Alimentos. RIL editores. https://www.digitaliapublishing.com/a/113096/topicos-en-microbiologia-e-inocuidad-de-los-alimentos
Obajemihi, O. I., Esua, O. J., Cheng,
J. H., & Sun, D. W. (2023). Effects of pretreatments using plasma
functionalized water, osmodehydration and their combination on hot air drying efficiency
and quality of tomato (Solanum lycopersicum L.) slices. Food Chemistry,
406(November 2022), 134995. https://doi.org/10.1016/j.foodchem.2022.134995
Petrotos, K. B., & Lazarides, H.
N. (2001). Osmotic concentration of liquid foods. Journal of Food
Engineering, 49(23)(201–206), 1–6. https://doi.org/10.1016/S0260-8774(00)00222-3
Pinzon, M. I., Villa, C. C., &
Nieto, J. A. (2011). Cambios de color y perfil aromático en soluciones osmóticas
usadas en deshidratación osmotica de tomate de árbol. Biotecnología en el
Sector Agropecuario y Agroindustrial 9(2), 121-129. http://hdl.handle.net/11336/190501
Sacchetti, G; Gianotti, A; Dalla
Rosa, M.; (2001). Sucrose-salt combined effect on mass transfer kinetics and
product acceptability. Study on apple osmotic treatment. Journal of Food Engineering,
47, 163-173. https://doi.org/10.1016/S0260-8774(00)00206-5
Suárez-Morales, J. A.,
Hernández-Arriola, D. G., Marín-Benítez, M. E., & Riera-González, G.
(2021). Deshidratación osmótica de la piña var. española roja para su
incorporación a una leche fermentada. Ciencia y Tecnologia de Los Alimentos,
31(2), 47–52. https://revcitecal.iiia.edu.cu/revista/index.php/RCTA/article/view/276/237
Villa, C. C., Nieto, J. A., &
Pinzón, M. I. (2009). Cambios composicionales y microbiológicos asociados a
ciclos sucesivos de deshidratación osmótica de tomate de árbol. Biotecnología
en el sector agropecuario y agroindustrial, 7(1), 29–35. http://www.scielo.org.co/pdf/bsaa/v7n1/v7n1a05.pdf
Zou, K., Teng, J., Huang, L., Dai,
X., & Wei, B. (2013). Effect of osmotic pretreatment on quality of mango
chips by explosion puffing drying. Lwt, 51(1), 253–259. https://doi.org/10.1016/j.lwt.2012.11.005